学生の頃から、2進数が苦手だった・・・。
浮動小数点も、本当のところはよくわからなかった・・・。
それがわからなくても、日常生活で苦労することは皆無だったし、
PCに触れている時でも、これと言って計算に困るような出来事もなかった。
そう、これまでは・・・
ただ、職場が変わって、状況が変化。
苦手だった2進数や、浮動小数点を、ほっとけなくなっちゃった・・・。
もくじ
1.10進数を2進数に変換
2.浮動小数点
3.0.1(10)を2進数に変換
4.まとめ
5.お願いとお断り
1.10進数を2進数に変換
これが苦手で、小テストとかあって、本当に困ってるひとが、もし、いたら、
僕なりに苦しい中から見出した絶対忘れない変換方法をお伝え出来たらと思って、
この記事を書いています。
まず、僕は、よく見るコレが『なぜか苦手』でした(今でも)。
例えば7(10)を2進数に変換する場合、

答えは、図の矢印の順に読んで、0111(2) 。だけど・・・
この書き方。すごく、思い出しにくい。
特に焦ったりすると、何か、どこかで混乱して、僕は必ず間違えてしまう。
自分なりに考えて出した「結論」は・・・この書き方、普段ほとんど使わないから・・・かな? みたいな
そこで、小学校以来慣れ親しんだ書き方がよかろうと思い、
自分では、より『素直』に思えるカタチに書き方を変更。
結果、これなら絶対間違えないと思えました。
自分的には、この書き方の方が、なぜかとても安心感があります。なんでかな?

自分に対して、自信が持てない本当の理由は、わかってます。
答えを出す方法だけが知りたくて、『なんで2で割り算するのか?』考えたことがなかったからです。
つまり、『ほんとうのこと』から、僕は目を反らし続けてきた・・・から。
理由はいくらでもあげられます。
めんどくさかったから
考えたくなかったから
試験に通ればそれでよかったし
そんなこと、どうでもよかったカラ
でも、とうとう、ここで、それは通用しなくなりました。
『2で割り算する』、その理由を僕は説明しなければならない。
誰もがわかるように・・・。
とりあえず、わかりやすい10進数で考えてみます。
10進数の基数は「10」、では基数で割り算するってどういうことなのか?

基数で割り算した余りが、元の10進数の一の位、十の位、百の位、千の位と一致します。
つまり、各「位(くらい)」の数を求めていたわけですね!
2進数の場合、基数は「2」ですから、基数で割り算すれば、余りは「0」か、「1」のいずれかになります。これが、その桁の2nが「あるか・ないか」を教えてくれるわけです。
例えば、10進数の「123」を2進数に変換する場合、

01111011(2)の0と1はそれぞれ、その桁の2nが「あるか・ないか」だから

電卓の種類を「プログラマー」に変更して、ラクして確認。
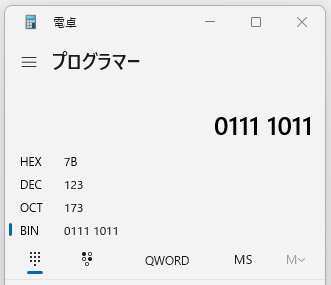
手計算でも確認(これが16進数で桁数が多かったら、挫けそうだなー)。
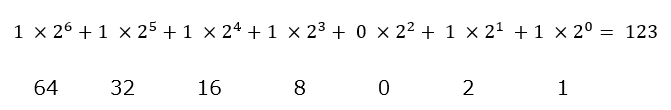
2進数でも、余りは、そのまま、各位(くらい)の数になりました。
よかった。よかった。
2.浮動小数点
数値のどこまでが信頼できる桁であるのかを表すのに、有効数字を用いますが、例えば
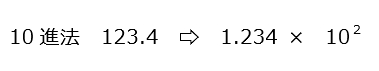
有効数字の 1.234 の部分を「仮数(かすう)」というそうです。
2進法では、次のような場合を考えると、
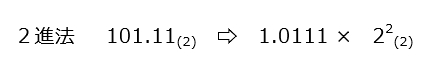
2倍すると1桁、位が上がりますから、2の2乗倍=4倍すれば2桁、位(くらい)が上がることになります。これを小数点の位置で言えば、2をかけるたびに、小数点の位置が右へ移動するわけです。
(だから「浮動小数点」って言うのかぁ・・・)
ここでの仮数は「1.0111」ですが、実は仮数には重要な決まりがあって、「整数部分を1桁とし、そこに0以外のいちばん上の位の数を置く」のだそうです(⇨ IEEE754 という方式に準拠した場合?)。
・・・と、いうことは、2進数なら「0」と「1」しかないから、仮数の整数部分は必ず「1」になることになります。
64ビットの浮動小数点数(2進数の場合)では、符号ビットは1ビット、指数部は11ビット、仮数部は52ビットで表わされることが多いそうで、符号は+とーのどちらかだから1ビットでOKとして、仮数部ではその整数部分「1」を省略してしまうとのこと。なんで?
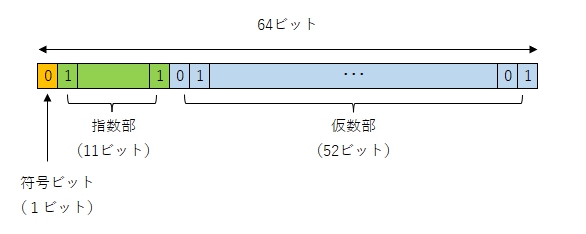
仮数部で整数部分の「1」を省略する理由がわからなかったので調べてみました。結果を知って納得。
整数部分の1を省略すれば、仮数部を1ビット増やすことができるので、浮動小数点形式の精度を向上させることができる。
(すごーい!)
仮数の整数部分を必ず「1」とすることで、そんなことも可能になるわけですね!
3.0.1(10)を2進数に変換
すーぱー 苦しんだのが、コレです。
10進数の小数を2進数に変換するなんて、もう長いことやってない。
やったことがあるとしても、15年以上前です。その記憶の欠片すら、残ってません。
表し方を調べてみると・・・、整数でやったコレを、そのまま2のマイナス1乗みたく、右側へ拡張して小数点以下を表現するとのこと。
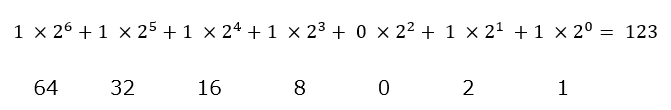
そー言えば、はるか、むかし。
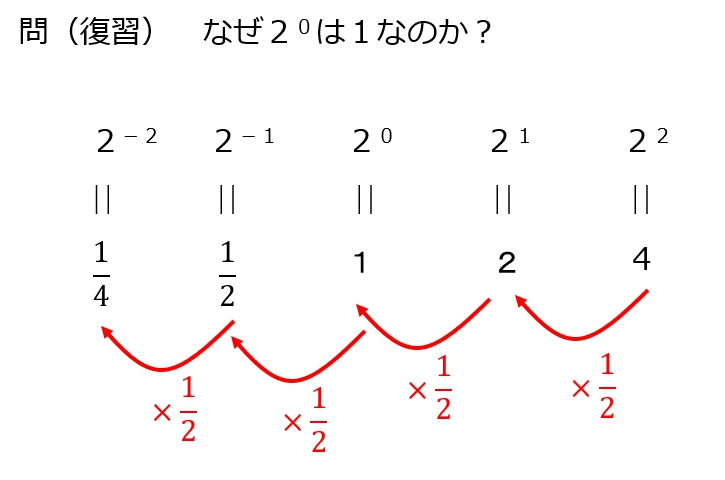
なんで2のゼロ乗が1になるのか、さっぱりわからず、悩んだことがあったよーな・・・。
わかってみれば、カンタンだったけど。
この関係を含めて10進数の小数を位(くらい)の数として表せば、

2進数でも、考え方は同じ。
違うのは、それがいくつあるか? ではなく、単に「ある」か・「ない」か が、「ある」=「1」、「ない」=0で示されること。あとあと、これがかなり重要な理解のポイントになります!

特に、0.X とした場合の小数点以下の部分 は(1の位が0であることを明示して表せば)、

この関係がそのまま使えれば、話はカンタン。
例えば10進数の 0.625 を2進数に変換したい場合、0.625 が 0.5 と 0.125の和であることに気付けば、
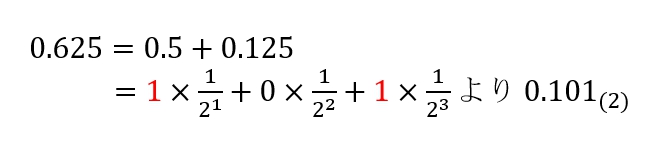
んじゃ、10進数の 0.1 を2進数に変換するには?
理解のために、全桁「1」で数値が「ある」ものとし、位(くらい)の数を書き出して考えます・・・

2進数で計算すると、このような誤差が必ず生まれてしまう!
だから、0.1 に少しずつ近づくように(0.1 を超えないように)、足し算可能な、よりちいさな数を求め、どこまでもこれを繰り返して(=循環する理由)行くわけですか・・・
(それはわかったけど、0.1(10) を2進数に変換するわかりやすい方法は・・・)
Google先生に、いろいろたずねても、コレだぁ!・・・みたいな答えは教えてくれない!!
それでも、いろんなWebサイトさんの断片的な情報を集めて、ようやく変換方法だけはわかりました☆
それが、こちら(10進数の 0.1 を2進数に変換)

なんで、これで変換できるのか?
次の式を書き出して、ひたすら考えます・・・(この場合、左辺のxは もちろん 0.1)。
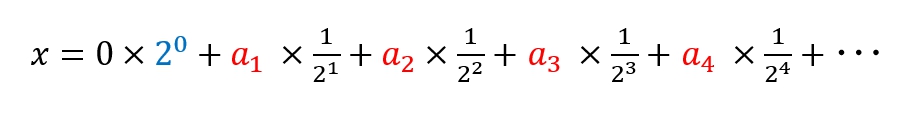
10進数の 0.1 を2進数に変換するとき、なんで割り算でなく、基数を掛け算してるのか? まず、それがさっぱりわからないけれど、ここでまず思い出したことは、これは2進数表現だから、an は必ず0か1のいずれかになるということ。
つまり、an が「1」ならその部分は数値が「あり」で、an が「0」なら「ない」わけです。
一歩、前進。
問題は基数を「掛け算」する理由。
基数を掛け算する・・・、つまり、2倍するってことは、意味的にはナニをしているのかというと、2倍して1桁、位を上げていることになる。おそらく、この部分に重大な意味があるような気が・・・。
てか、ナンで桁を上げる必要があるのか?
それがアタマにこびりついて、離れません。
(あぁ ナニを見ても0と1に見える・・・)
誰か、教えてくれないかなー
ブラウザのタブを切り替えながら、既に何度も眺めたWeb上の情報にもう一度目を通します。
(なにか、見落としてること、あるんじゃないかなー)
あるWebサイトにあった次の文がなぜかキラキラ輝いて見えます。でも、なんで輝いて見えるのか、それがわかりません。
2進数で表された1.0と、10進数で表された1.0は、数の重みが等しい(同じ数!)
なんか、ものすごく大切なことを伝えてくれている気がするのですが、その「ものすごく大切なこと」がナンなのか? それがどうしてもわかりません!
0.1 かぁ・・・ これは10進数の小数で・・・
それを2進数にしたいんだよなぁ・・・

左辺の 0.1 は、10進数の領域にあって・・・、右辺は、2進数の領域にあると考えれば・・・
右辺のan は絶対に「1」か「0」のどちらかになる(2進数だから)。
「1」なら「数値あり」で、「0」なら「ない」。
で・・・
a1 は2倍すれば、一の位に現れる・・・
a2 は22=4倍すれば、一の位に現れる・・・
a3 は23=8倍すれば、一の位に現れる・・・
2進数も、10進数も、一の位だけは・・・1が意味合い的に同じ「ひとつだけあるの1(イチ)」。
・・・って、コトは、
二つの異なる領域をイコールで結ぶために必要な、その条件が一の位・・・
そうか、一の位じゃないと・・・「0」か、「1」かが、きっと 見えない んだ!
だから、どんどん2倍して、
a1、a2、a3・・・が、次々に一の位になるように、桁を上げるんだ☆
一の位になって初めて、それが「0」なのか、「1」なのかが 見える んだ!!
あー☆ わかったカモー!!

だから、(上の計算で)基数を掛け算した結果、整数部に「1」が出てきた時は、それが「ある」ことさえわかればイイから、その存在を無視して、小数部だけを基数倍(2倍)してるんだ!
コレ、考えた人、天才だ☆
4.まとめ
今回は内容が多岐にわたり、コレが最も適切かと・・・思われます。
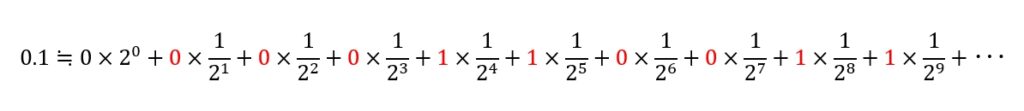
5.お願いとお断り
このサイトの内容を利用される場合は、自己責任でお願いします。ここに記載した内容を利用した結果、利用者および第三者に損害が発生したとしても、このサイトの管理者は一切責任を負えません。予め、ご了承ください。